BASE
个人认为是基础算法中最难的部分, 常常被用来求解最优问题.
学习动态规划问题首先要知道什么时候用动态规划,可不仅仅是只能用在求解最优的时候. 个人认为是当我们会遇到很多选择,并且之前的选择会对之后的选择产生影响的时候.
也就是通过记录一些中间状态逐步推出最终状态
无论是背包问题中选择物品, 还是在地下城问题中选择路线, 还是正则表达式匹配中选择当前是否再匹配一次*. 这些问题中都有大量的选择
而且之前的选择会对之后产生影响. 例如之前选择的物品会占用背包的体积影响之后能否放下新的物品; 地下城问题中之前的选择会决定所需的血量; 正则匹配中只有之前可以全部正确的匹配的选择才能继续匹配.
动态规划就是把这些选择都记录下来, 再依据之前的选择推出后面的选择, 这就是动态规划的核心: 用小问题推导出最终问题
其次是动态规划应该怎么做, 这里当然有标准解答
-
状态: 记录的到底是什么, 也就是说选择带来的结果
-
转移方程: 怎样可以记录当前的状态
-
特殊情况: 在最初或者是最后常常都有特殊情况出现
动态规划其实就是通过这个三点就可以去每次选择最优子结构, 进而得到最后的最优解
但具体情况肯定还是要看case的, 那么接下来就通过下面几道题来逐步理解动态规划的做法吧!
CASE
01背包问题
基础背包问题
对于一组不同重量、不可分割的物品,我们需要选择一些装入背包,在满足背包最大重量限制的前提下,背包中物品总重量的最大值是多少呢?
我们假设背包的最大承载重量是 5。我们有 3 个不同的物品,每个物品的重量分别是 w = {2,4,3}
这里将不和大多数文章一样和递归进行比较, 我们直接使用动态规划的思想考虑问题, 也就是记录状态, 进而推出最终状态
但是这里我们应记录怎样的状态呢? 这就是动态规划解法第一步需要得到的答案. 刚开始解除动态规划问题, 可能比较难直接理解状态, 这里我们从拆解问题说起. 回顾开篇我们说过的, 用小问题推出大问题. 这里怎么拆分小问题呢? 我们有2个条件, 物品和背包. 拿什么物品是我们要做出的选择而背包体积我们可以进行拆分
-
我们把整个求解过程
拆分为 w 个阶段(w 表示背包的容积),每次我们都会增大1点背包的容积, 并计算当前容积下背包最大可以放多少东西 -
每个物品做出
选择(放入或者不放入背包)之后,背包中的物品的重量会有多种情况,也就是说,会达到多种不同的状态. 而每一层的状态个数也就是我们可以尝试是否放进背包的物品个数 n 个(n 表示可选择物品的个数)
这里拆分任务, 并作出选择后, 我们就可以得到每一步的状态. 我们可以用一个二维数组 dp[w+1][n+1],来记录每次可以计算出的状态。这就是第一个核心点 记录状态. 而 dp[i][j] 记录的状态就是在容积为 i 并且使用 j 件物品的时候能达到的最大容积.
我们可以基于上一层的状态集合,来推导下一层的状态集合. 则也就是建立转移方程的过程.
把记录状态的数组如果画成一个表就可以更清晰的表述由之前的状态推出后面的状态的过程.
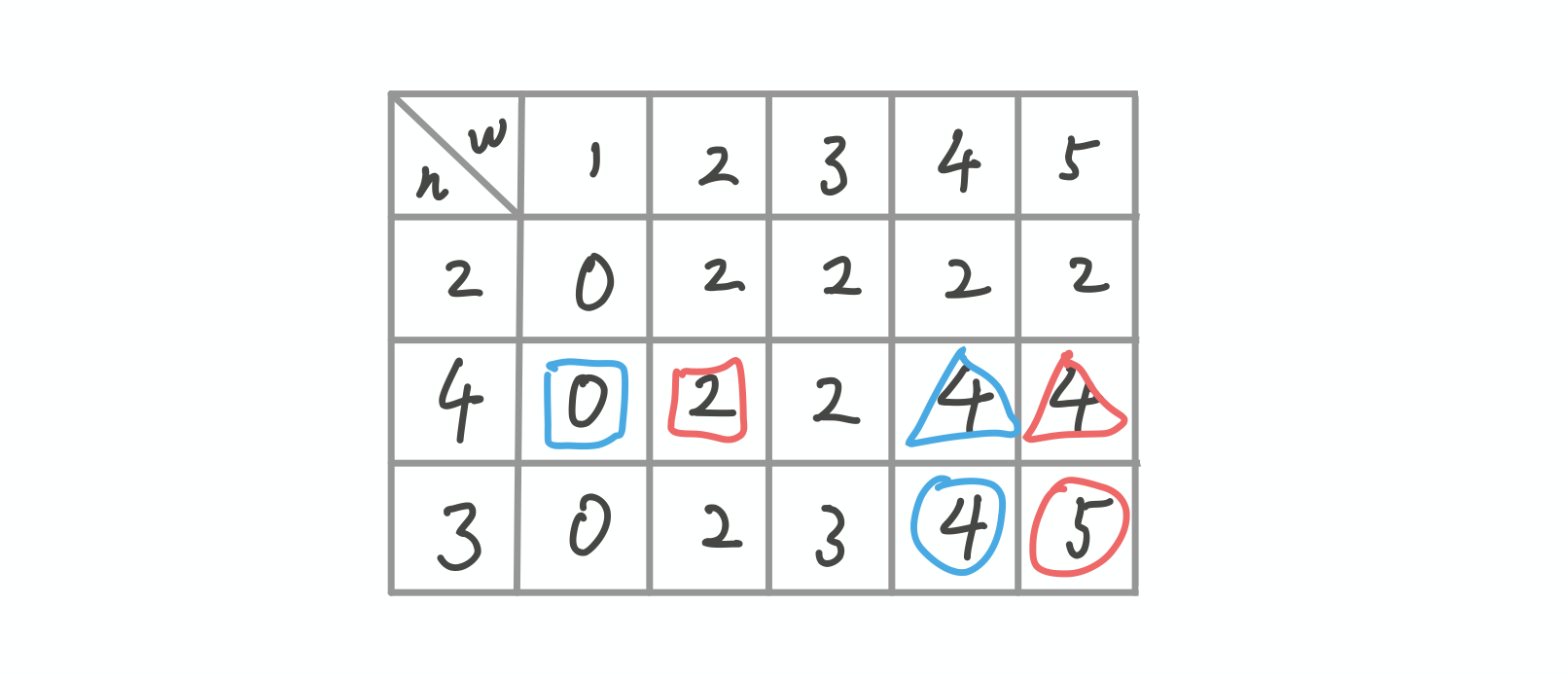
我们来分析一下上图, 每次我们在考虑是否将当前物品放进去的时候, 看到会比较放入当前总重量比较大还是不放入当前总重量比较大. 我们通过分析两个case说明怎样进行状态转移
-
蓝色圈的位置是由: 蓝色三角位置(4 -> 不选择放入该次物品) 与 蓝色正方形的位置(0 -> 放入该次物品剩余容积还可以放入的最大重量) + 该次物品的重量(3 -> 放入该次物品) => 4 (显而易见还是不放入要大一点)
-
最终红圈位置是由: 红色三角位置(4 -> 不选择放入该次物品) 与 红色正方形的位置(2 -> 放入该次物品剩余容积还可以放入的最大重量) + 该次物品的重量(3 -> 放入该次物品) => 5 (最终可以得到放入该次物品后剩下的2点容积可以正好再放重量为2的物品)
通过以上分析, 我们就可以来建立三要素了:
-
状态:
dp[i][j]记录的状态就是在使用 i 件物品并且容积为 j 的时候能达到的最大容积 -
转移方程:
dp[i][j] = max(dp[i - 1][j], weights[i] + dp[i - 1][j - weights[i]])这里的weights[i]代表第 i 件物品的重量 -
特殊情况: 因为会从背包重量为1开始考虑, 势必会出现背包重量放不下当前物品的情况, 也就是
weights[i] <= j这样直接使用dp[i - 1][j]即可. 还有一种特殊情况是i - 1不越界, 其实很简单从i=1开始循环即可.
接下来代码就横容易实现了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private int backage(int[] weights, int w) {
int n = weights.length;
// 这里都+1是为了考虑i-1不会越界的情况
int[][] dp = new int[n + 1][w + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= w; j++) {
if (j >= weights[i - 1]) {
dp[i][j] = Math.max(dp[i - 1][j - weights[i - 1]] + weights[i - 1], dp[i - 1][j]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][w];
}
价值背包问题
刚刚我们的物品只有一个条件就是重量, 如果物品还有价值呢? 其实很简单状态变为物品的价值就好了, 其他的就很好考虑了
这里用一种优化解法, 对于刚刚的背包问题其实我们只用到了 i - 1 行来推出当前行. 所以只要缓存前一行就可以了.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int getMoreGold(int weight, int[] costs, int[] weights) {
int[] tmp = new int[weight + 1];
int[] result = new int[weight + 1];
for (int i = 0; i < weights.length; i++) {
// 内层循环为人,一行从左到右一个一个算,也就是逐渐增加人数
for (int j = 0; j <= weight; j++) {
if (weights[i] <= j) {
result[j] = Math.max(tmp[j], costs[i] + tmp[j - weights[i]]);
}
}
tmp = result.clone();
}
return result[result.length - 1];
}
这里weight还是背包容积, weights物品重量数组, costs则是对应的利润. tmp就是i-1层的状态记录, 而result是当前记录.
01背包是最经典的动态规划问题. 如果让我分类, 我会把动态规划分为1维问题和2维问题, 背包问题也属于二维问题. 接下来就按照这个分类来看case
一维问题
一维问题是最基础的动态规划问题, 只需要一层循环就可以解决问题. 例如最爬楼梯问题. 但也有稍微复杂的情况, 比如下面的最长有效括号问题.
最长有效括号问题
当遇到)时构建状态转移方程进行求解f(i)=max[之前最长,这次的长度]
状态: dp[i] 当前位置为结算的最长有效括号长度. 这个有点绕, 其实就是每次能组成有效括号的时候记录一下当前的有效括号长度, 而如果没记录则为0.
转移方程: 这里有2中情况, 核心是依据状态在当前是)的时候进行计算
-
···()的情况, 这种情况i-1就是(也就是说直接在i-2位置记录长度的基础上+2, 当然i-2的位置根本不是有效括号1
dp[i] = dp[i - 2] + 2
-
···(···)的情况, 这里要求括号中的···都是有效括号. 这里要计入两种有效括号长度. 一个是和刚刚一样的, 这次有效括号前面的记录长度dp[i - dp[i - 1] - 2]. 另一部分则是该次有效括号总计的匹配长度dp[i - 1]. 这两个记录再加上2就是本次的长度了1
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2
是不是很复杂, 这道题就是需要考虑的情况非常多. 而且还没有结束, 还需要定义特殊情况
特殊情况: 这里的特殊情况其实很简单, 只要考虑数组越界就好了, 也就是如果之前的···根本不存在肯定要特殊处理一下.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int longestValidParentheses(String s) {
int maxans = 0;
int dp[] = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] +
((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
二维问题
二维动态规划问题简单来说就是需要建立二维数组记录状态, 进而求解. 这也是大多数动态规划问题的解法. 最初举例的背包问题也是二维问题, 仅仅是因为它太典型了才拿来放在最前面
地下城问题
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
1
2
3
-2, -3, 3
-5, -10, 1
10, 30, -5
关键是要逆推求解
1
2
3
-5(6) 30(1) 10(1)
1(5) -10(11) -5(6)
3(2) -3(5) -2(7)
上图是逆向的地下城图, 和上图正好是对称的. 括号中就是勇士从这里出发最少需要的血量. 以本应该是最后一步的-5来说, 如果是直接走到最后一步则需要的血量是6点. 进而在1位置的时候, 因为可以加一点血, 所以5点血就够了.
如果是-3的位置, 我们有两个选择. 可以走到-10也可以走到3的位置, 这里就可以比较下如果从那个位置开始走, 哪个需要的血量少. 显而易见3的位置只需要2点血就可以通关, 在加上这里所需的3点血, 就得到了5点血的结果.
以此推算, 直到真正的起点-2处, 就应该需要7点血
在上面的推算过程中, 其实我们已经得到了状态转移方程
1
blood[i][j] = Math.min(blood[i + 1][j], blood[i][j + 1]) - dungeon[i][j];
当前所需最少血量为, 下面能走的两部中需要血量最少的再减去这里消耗的血量就是当前位置所需的最少血量了. 当然我们还需要加上边界条件, 最终就可以得到实现代码了.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private int calculateMinimumHP(int[][] dungeon) {
int rowLen = dungeon.length;
int colLen = dungeon[0].length;
int[][] blood = new int[rowLen][colLen];
for (int i = colLen - 1; i >= 0; i--) {
for (int j = rowLen - 1; j >= 0; j--) {
if (i == rowLen - 1 && j == colLen - 1) {
blood[i][j] = dungeon[i][j];
} else if (i == rowLen - 1) {
blood[i][j] = blood[i][j + 1] + dungeon[i][j];
} else if (j == colLen - 1) {
blood[i][j] = blood[i + 1][j] + dungeon[i][j];
} else {
blood[i][j] = Math.max(blood[i + 1][j], blood[i][j + 1]) + dungeon[i][j];
}
// 最多为不扣血
blood[i][j] = Math.min(0, blood[i][j]);
int i1 = 1 - blood[i][j];
System.out.print(dungeon[i][j] + "(" + i1 + ") ");
}
System.out.println();
}
return 1 - blood[0][0];
}
通过上述问题可以发现, 他们都是最优解问题. 也是动态规划最经典的使用场景. 最优解问题通常会用
max函数进行比较得到当前的最优解
正则表达式匹配
给出一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ’*‘ 的正则表达式匹配。
’.’ 匹配任意单个字符 ‘*’ 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。 p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
1
2
3
4
5
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')
分析题目
该题并不是最优解问题了, 那为什么是动态规划问题呢? 其实在我们分析题目的时候就能发现.
这道题的难点在于*字符, 因为其可以匹配零到多个字符. 也就是说匹配几个字符都有可能. 这样就需要尝试匹配0到多次. 每次都面临多种选择. 而且每次是否能继续匹配除了当前能否匹配成功以外, 还需要保证已经匹配过的都是可以匹配上的, 需要用之前记录的状态影响之后的状态判断.
以上不正是动态规划的标准题型吗? 动态规划循环的意义在于尝试每一种选择的情况, 进而依据之前的选择进行推出之后的选择.
首先还是要建立状态转移方程
-
状态: dp[i][j] 表示 text 从 i 开始到最后,pattern 从 j 开始到最后,此时 text 和 pattern 是否匹配
-
转移方程: 我们就可以依据我们刚刚分析过的选择建立状态转移方程.
-
当前后一位不是
*: 当前的text和pattern匹配 且dp[i + 1][j + 1]为true (按照我们设定的状态这里代表了ext 从i+1开始到最后,pattern 从j+1开始到最后,可以匹配) -
当前后一位是
*:dp[i][j + 2]为true (代表了跳过*和前一位字符) 或者 是当前的text和pattern匹配(保证当前可匹配上) 且dp[i + 1][j]为true (text后面都已经匹配上) 即, 尝试当前不匹配 或者 尝试再匹配一位
-
之后是考虑特殊情况
我们的状态是i,j之后都是匹配成功的, 那势必要考虑第一次循环的时候怎么知道状态是什么. 这里也是动态规划法常用的解决思路.
1
boolean[][] dp = new boolean[text.length() + 1][pattern.length() + 1]
dp数组的长度增加一位来记录初始特殊情况, 在这道题也就是两边为空的情况.
-
两边都为空 -> true [初始化特殊情况]
-
text为空, 如果pattern为
x*(x代表任意字符), 则可以匹配0次 -> true [在循环中判断] -
pattern为空, text不为空 -> false [直接跳过全为false]
这两步清楚后代码就很简单了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private boolean isMatchR(String text, String pattern) {
// 多一维的空间,因为要考虑两边为空的情况进行匹配(这就是动态规划中的特殊情况处理, 在判断的时候会用到这些特殊情况)
// 当然如果text不为空, p为空则肯定匹配不上, 所以可以忽略, 因为定义的数组默认都是False
// dp[i][j]dp[i][j]表示 text 从 i 开始到最后,pattern 从 j 开始到最后,此时 text 和 pattern 是否匹配。
boolean[][] dp = new boolean[text.length() + 1][pattern.length() + 1];
// dp[len][len] 代表两个空串是否匹配了,"" 和 "" ,当然是 true 了。
dp[text.length()][pattern.length()] = true;
// 为什么text要从len开始减少, 是因为要匹配一圈text为空的情况.
for (int i = text.length(); i >= 0; i--) {
for (int j = pattern.length() - 1; j >= 0; j--) {
boolean first_match = i < text.length() && (pattern.charAt(j) == text.charAt(i) || pattern.charAt(j) == '.');
if (j + 1 < pattern.length() && pattern.charAt(j + 1) == '*') {
dp[i][j] = dp[i][j + 2] || first_match && dp[i + 1][j];
} else {
dp[i][j] = first_match && dp[i + 1][j + 1];
}
}
System.out.println();
}
return dp[0][0];
}
以上是逆推的做法, 当然也可以正推出来.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private boolean isMatchS(String s, String p) {
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
dp[0][0] = true;
// sl/pl 代表的是长度, 因为要考虑长度为0的情况
// i,j代表的是字符匹配到的位置
// dp[sl][pl] 代表长度为sl,pl之前都可以匹配 -> 状态
// sl,pl 长度都为0可以匹配 -> 特殊1
// p为空 s不为空肯定都匹配不上 所以要考虑s为空p不为空的所有情况 s从长度为0开始循环 -> 特殊2
for (int sl = 0; sl <= s.length(); sl++) {
for (int pl = 1; pl <= p.length(); pl++) {
int i = sl - 1, j = pl - 1;
if (sl == 0) {
dp[sl][pl] = p.charAt(j) == '*' && dp[sl][pl - 2];
} else if (p.charAt(j) == '*') {
boolean singleMatch = s.charAt(i) == p.charAt(j - 1) || p.charAt(j - 1) == '.';
dp[sl][pl] = singleMatch && dp[sl - 1][pl] || dp[sl][pl - 2];
} else {
boolean singleMatch = s.charAt(i) == p.charAt(j) || p.charAt(j) == '.';
dp[sl][pl] = singleMatch && dp[sl - 1][pl - 1];
}
}
}
return dp[s.length()][p.length()];
}
以上常规case基本都提到了, 接下来如果有新的case会增加在后面
最长回文字串
该提的关键是由长度为0开始循环, 核心也是找到3要素
状态: 开始位置为
start结算位置为end的字符串是回文字串转移方程: P[start + 1][end - 1] && s.charAt(start) == s.charAt(end)
特殊情况: len=1 一定为true 而 len=2 只需要判断 s.charAt(start) == s.charAt(end)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public String longestPalindrome(String s) {
int length = s.length();
boolean[][] P = new boolean[length][length];
int maxLen = 0;
String maxPal = "";
for (int len = 1; len <= length; len++) //遍历所有的长度
for (int start = 0; start < length; start++) {
int end = start + len - 1;
//下标已经越界,结束本次循环
if (end >= length) break;
//长度为 1 和 2 的单独判断下
P[start][end] = (len == 1 || len == 2 || P[start + 1][end - 1])
&& s.charAt(start) == s.charAt(end);
if (P[start][end] && len > maxLen) {
maxPal = s.substring(start, end + 1);
}
}
return maxPal;
}